Bảy hằng đẳng thức đáng nhớ và một số mẹo nhớ siêu nhanh

“Bảy hằng đẳng thức đáng nhớ” là những đẳng thức cơ bản nhất mà mỗi người học toán cần phải nắm vững, là tiền đề của những kiến thức trong toán cấp 2 và toán cấp 3.

• “Tuyệt chiêu” xử gọn mọi bài tập Hình học Kỳ thi THPT Quốc Gia năm 2020
• 6 sai lầm dễ mất điểm khi làm bài thi môn Toán vào lớp 10
• Một số lưu lý quan trọng khi ôn thi kỳ tuyển sinh vào lớp 10 môn toán

Bảy hằng đẳng thức đáng nhớ và một số mẹo nhớ siêu nhanh

“Bảy hằng đẳng thức đáng nhớ” – chỉ nghe tên gọi cũng đã biết đây là một lời nhắc nhở chúng ta cần phải ghi nhớ chúng một cách lâu dài, bởi những đẳng thức này được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia các đa thức, biến đổi biểu thức tại cấp học THCS và THPT.

Vậy “Bảy hằng đẳng thức đáng nhớ” là gì? Làm sao để có thể ghi nhớ chúng chính xác, nhanh chóng và nhớ lâu chúng, hãy cùng Toán cấp 3 tìm hiểu và luyện tập qua bài viết này nhé.

Bảy hằng đẳng thức đáng nhớ là gì?

“7 hằng đẳng thức đáng nhớ” là những đẳng thức cơ bản nhất mà mỗi học sinh khi học toán cần phải nắm vững. Các đẳng thức này được xây dựng và chứng minh bằng cách nhân đa thức với đa thức. Học thuộc 7 hằng đẳng thức đáng nhớ giúp giải nhanh những bài toán phân tích đa thức thành nhân tử.

Sau đây là 7 hằng đẳng thức đáng nhớ chúng ta cần phải học thuộc:

1. Bình phương của 1 tổng:

• (a + b)² = a² + 2ab + b² = (a – b)² + 4ab
• Giải thích công thức bằng lời: Bình phương của một tổng bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất nhân với số thứ hai, cộng với bình phương của số thứ hai

2. Bình phương của 1 hiệu:

• (a – b)² = a² – 2ab + b² = (a + b)² – 4ab
• Giải thích công thức bằng lời: Bình phương của một hiệu bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất nhân số thứ hai sau đó cộng bình phương với số thứ hai.

3. Hiệu 2 bình phương:

• a² – b² = (a – b)(a + b)
• Giải thích: Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.

4. Lập phương của 1 tổng:

• (a + b)³ = a³ + 3a²b + 3ab² + b³
• Giải thích bằng lời: Lập phương của một tổng hai số bằng lập phương của số thứ nhất cộng với ba lần tích bình phương số thứ nhất nhân số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai cộng với lập phương số thứ hai.

5. Lập phương của 1 hiệu:

• (a – b)³ = a³ – 3a²b + 3ab² – b³
• Giải thích bằng lời: Lập phương của một hiệu hai số bằng lập phương của số thứ nhất trừ đi ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai trừ đi lập phương số thứ hai

6. Tổng 2 lập phương:

• a³ + b³ = (a + b)(a² – ab + b²) = (a + b)³ – 3a²b – 3ab² = (a + b)³ – 3ab(a + b)
• Giải thích bằng lời: Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó

7. Hiệu 2 lập phương:

• a³ – b³ = (a – b)(a² + ab + b²) = (a – b)³ + 3a²b – 3ab² = (a – b)³ + 3ab(a – b)
• Giải thích bằng lời: Hiệu của hai lập phương của hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.

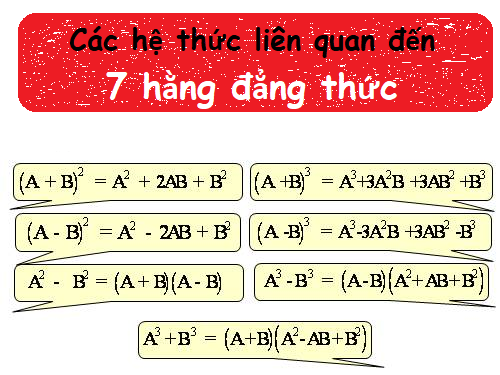
Một số hệ thức liên quan đến 7 hằng đẳng thức đáng nhớ

Các hệ thức liên quan đến 7 hằng đẳng thức

Hằng đẳng thức mở rộng với hàm bậc 2

• (a – b – c)² = a² + b² + c² – 2ab + 2bc – 2ac
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac
• (a + b – c)² = a² + b² + c² + 2ab – 2bc – 2ac

Hằng đẳng thức mở rộng với hàm bậc 3

• a³ + b³ = (a + b)³ – 3ab(a + b)
• a³ – b³ = (a – b)^{3 +} 3ab(a – b)
• (a + b + c)³ = a³ + b³ + c³ + 3(a + b)(b + c)(a + c)
• a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ac)
• (a – b)³ + (b – c)³ + (c – a)³ = 3(a – b)(b – c)(c – a)
• (a + b)(b + c)(c + a) – 8abc = a(b – c)² + b(c – a)² + c(a – b)²
• (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) – abc

Hằng đẳng thức dạng tổng quát

• aⁿ + bⁿ = (a + b)(a^n-1 – a^n-2 b + a^n-3 b_² – a^n-4 b³ + … + a²b^n-3 – ab^n-2 + b^n-1)
• a^{n –} bⁿ = (a – b)(a^n-1 + a^n-2 b + a^n-3 b_² + a^n-4 b³ + … + a²b^n-3 + ab^n-2 + b^n-1)
• Với n là số lẻ thuộc N (tập hợp số tự nhiên)

Nhị thức Newton

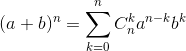
Với a,b thuộc tập hợp số thực (R), n thuộc tập hợp số tự nhiên dương (N*)

Trong những hằng đẳng thức này, 1 bên dấu bằng là tổng hoặc hiệu và bên gọi lại là tích hoặc lũy thừa. Những đẳng thức này luôn được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia đa thức, biến đổi biểu thức tại từ cấp 2 đến cấp 3 và 7 hằng đẳng thức đáng nhớ được in trong sách giáo khoa và được in rất nhiều trong bìa sau của vở viết cấp II hoặc cấp III của học sinh.

Mẹo ghi nhớ 7 hằng đẳng thức siêu nhanh và siêu lâu

Một số mẹo giúp ghi nhớ siêu nhanh và siêu lâu “7 hằng đẳng thức đáng nhớ”

Mẹo khác dấu

Giảng viên Trường Trung học phổ thông Sài Gòn bật mí về cách ghi nhớ “7 hằng đẳng thức” bằng mẹo khác dấu như sau: Nếu để ý, ta có thể nhận thấy rằng, các hằng đẳng thức: Bình phương của 1 tổng và 1 hiệu; Lập phương của 1 tổng và 1 hiệu; Tổng và Hiệu 2 lập phương đều khá tương tự nhau, chỉ khác nhau ở dấu. Vì vậy điều cần lưu ý ở đây chính là ghi nhớ dấu của chúng, từ đó ta có thể học thuộc một cách chính xác và không bị nhầm lẫn.

Đối với hằng đẳng thức Lập phương của 1 hiệu và Tổng 2 lập phương thì cần lưu ý đó chính là:

• “ Hiệu các lập phương bằng tích của hiệu hai số và bình phương thiếu của một tổng”
• “Tổng các lập phương bằng tích của tổng hai số và bình phương thiếu của một hiệu”

Học thuộc hằng đẳng thức qua bài hát chế

Toán học không phải là một môn học khô khan nếu chúng ta biết cách kết hợp giữa toán và văn, văn và toán thì thật sự là một điều rất tuyệt vời. Điều này không chỉ giúp chúng ta có cảm hứng học tập hơn mà còn giúp chúng ta ghi nhớ bài học một cách dễ dàng.Những bài hát hài hước, vui nhộn liên quan đến kiến thức học, giúp não bộ tiếp thu tốt hơn, một minh chứng cụ thể là 7 hằng đẳng thức đáng nhớ thay vì khó học với các con số, người ta thay chúng bằng phiên bản qua bài hát “Sau tất cả” với nội dung liên quan đến các hằng đẳng thức, thu hút được sự chú ý cũng như sự thích thú của nhiều bạn trẻ, phục vụ trong việc nhớ kiến thức lâu dài.

Mặc dù có nhiều mẹo để ghi nhớ công thức khác nhau nhưng cách tốt nhất để ghi nhớ công thức đó chính là không ngừng rèn luyện, luyện tập và làm bài tập chăm chỉ. Như vậy, chúng ta không cần ghi nhớ chúng một cách máy móc mà còn giúp chúng ta luyện tập thêm được nhiều dạng bài toán, chuẩn bị được hành trang vững chãi nhất để “chiến đấu” với những kỳ thi quan trọng sắp diễn ra. Chúc tất cả các bạn may mắn và thành công!

Nguồn: toancap3.com tổng hợp