Cách tìm giao tuyến của hai mặt phẳng

Cách tìm giao tuyến của hai mặt phẳng như thế nào? Để tìm được giao tuyến của hai mặt phẳng thì cần phải có những kiến thức cơ bản ra sao?

+ Phải nắm được định nghĩa về giao tuyến của hai mặt phẳng: Giao tuyến của hai mặt phẳng là đường thẳng chứa tất cả điểm chung của hai mặt phẳng đó

+ Phải nắm được các định lý và hệ quả về giao tuyến của hai mặt phẳng:

– Định lý về 3 mặt phẳng cắt nhau: Nếu 3 mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thi ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Từ đó ⇒ Hệ quả: Nếu hai mặt căt nhau lần lượt đi qua hai đường thẳng song song thì giao tuyến của hai mặt phẳng đó song song với hai đường thẳng hoặc trùng với một trong hai đường thẳng.

– Định lý 1 đường thẳng thuộc 1 mặt phẳng mà song song với 1 mặt phẳng: Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a mà cắt (P) thì cắt theo giao tuyến song song với a.

Từ đó ⇒ Hệ quả: Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với mặt phẳng đó.

* Chú ý: Để xác định một đường thẳng ta cần biết được 2 điểm phân biệt thuộc đường thẳng đó hoặc biết một điểm thuộc đường thẳng và phương của đường thẳng. Do vậy, ta có thể xác định đường giao tuyến của 2 mặt phẳng bằng các phương pháp sau:

1. Phương pháp 1: Tìm hai điểm chung phân biệt của hai mặt phẳng

Đường thẳng nối hai điểm chung đó chính là giao tuyến của hai mặt phẳng.

Ví dụ 1: Cho điểm S không thuộc mặt phẳng chứa hình thang ABCD (AB // CD và AB > CD). Tìm giao tuyến hai mặt phẳng (SAD) và (SBC).

Giải:

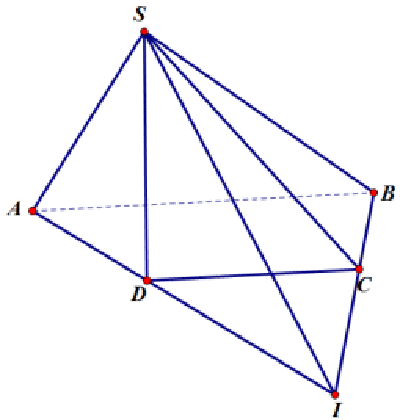
Dễ dàng thấy rằng, điểm S là một điểm chung của hai mặt phẳng (SAC) và (SBD).

Như vậy, để xác định giao tuyến của hai mặt phẳng này, ta chỉ cần tìm thêm một điểm chung nữa.

Ta thấy, AB > CD. Kẻ đường thẳng AD cắt đường thẳng BC tại I.

Khi đó:

I ∈ AD mà AD ⊂ (SAD) ⇒ I ∈ (SAD)

I ∈ BC mà BC ⊂ (SBC) ⇒ I ∈ (SBC)

Do đó, I là một điểm chung của hai mặt phẳng (SAD) và (SBC).

Vậy SI là giao tuyến của hai mặt phẳng (SAD) và (SBC).

Ví dụ 2: Cho Δ ABC nằm trong mặt phẳng (P) và đường thẳng a nằm trong mặt phẳng (P) không song song với AB, AC. S là một điểm nằm ngoài mặt phẳng (P) và A’ là một điểm thuộc SA. Xác định giao tuyến của hai mặt phẳng (A’; a) và (ABC).

Giải:

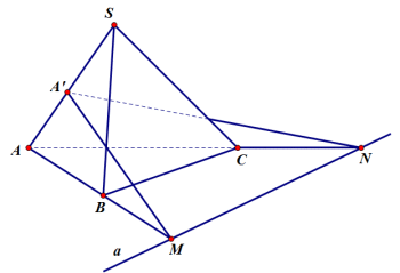
Kẻ đường thẳng AB cắt đường thẳng a tại M. Nối A’M. Khi đó,

A’M ⊂ (A’; a) và M ∈ (A’; a).

M ∈ AB mà AB ⊂ (ABC) ⇒ M ∈ (ABC)

Vậy M là một điểm chung của hai mặt phẳng (A’;a) và (ABC).

Kẻ đường thẳng AC cắt đường thẳng a tại N. Nối A’N. Khi đó,

A’N ⊂ (A’; a) và N’ ∈ (A’; a).

N ∈ AC mà AC ⊂ (ABC) ⇒ N ∈ (ABC)

Vậy N là một điểm chung của hạ mặt phẳng (Á’; a) và (ABC).

Do đó, MN là giao tuyến của hai mặt phẳng (A’; a) và (ABC).

2. Phương pháp 2: Tìm một điểm chung của hai mặt phẳng

Nếu hai mặt phẳng cần tìm giao tuyến lần lượt chứa hai đường thẳng song song thì giao tuyến cũng song song với hai đường thẳng đó.

Ví dụ 1: Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BP lấy điểm P sao cho BP = 2PD. Tìm giao tuyến của hai mặt phẳng (MNP) và (ABD).

Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Trên SD lấy điểm M. Tìm giao tuyến của (MBC) và (SAC).