Tính tích phân bằng phương pháp tích phân từng phần

Phương pháp tích phân từng phần cũng là một phương pháp được sử dụng rất nhiều trong các bài toán tích phân khó, có thể nói nó là phương pháp tối ưu.

Lý thuyết của phương pháp tích phân từng phần:

Nếu [latex]\displaystyle u(x)[/latex] và [latex]\displaystyle v(x)[/latex] có đạo hàm liên tục trên đoạn [a;b] thì:

[latex]\displaystyle \int\limits_{a}^{b}{u(x)}v'(x)dx=(u(x)v(x))\left| \begin{array}{l}b\\a\end{array} \right.-\int\limits_{a}^{b}{v(x)}u'(x)dx[/latex]

hay [latex]\displaystyle \int\limits_{a}^{b}{udv=}uv\left| \begin{array}{l}b\\a\end{array} \right.-\int\limits_{a}^{b}{vdu}[/latex]

Các em xem ví dụ dưới đây sử dụng phương pháp tích phân từng phần để giải.

Ví dụ 1: Tính tích phân I = [latex]\displaystyle \int\limits_{1}^{e}{x\ln xdx}[/latex]

Giải:

Đặt: [latex]\displaystyle \left\{ \begin{array}{l}u=\ln x\\dv=xdx\end{array} \right.[/latex]

[latex]\displaystyle \Rightarrow \left\{ \begin{array}{l}du=\frac{dx}{x}\\v=\frac{x_{{}}^{2}}{2}\end{array} \right.[/latex]

Khi đó I = [latex]\displaystyle \int\limits_{1}^{e}{x\ln xdx}=\frac{x_{{}}^{2}}{2}\ln x\left| \begin{array}{l}e\\1\end{array} \right.-\frac{1}{2}\int\limits_{1}^{e}{xdx}=\frac{e_{{}}^{2}}{2}-\frac{x_{{}}^{2}}{4}\left| \begin{array}{l}e\\1\end{array} \right.=\frac{e_{{}}^{2}+1}{4}[/latex]

*Chú ý: 

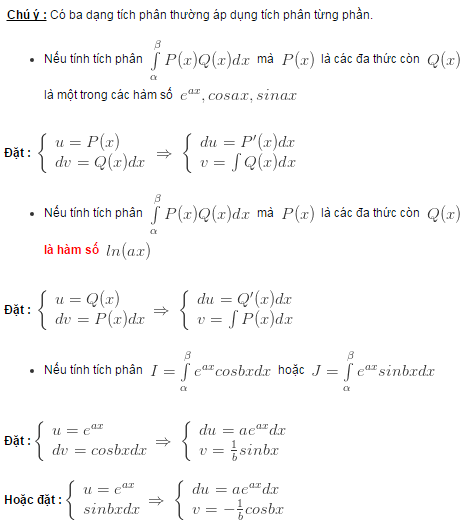
Bài viết hay liên quan: Tính tích phân bằng phương pháp đổi biến số