Một số dạng Toán về mặt phẳng và đường thẳng
Các bài toán về đường thẳng và mặt phẳng xuất hiện khá nhiều trong đề thi tuyển sinh vào đại học cao đẳng môn Toán từ trước tới nay.
Và dưới đây là Phương pháp giải và ví dụ bài tập về 4 dạng toán về mặt phẳng và đường thẳng mà các em cần ghi nhớ.
Dạng 1: Viết phương trình tham số và phương trình chính tắc của đường thẳng 
Phương pháp :
Xác định một điểm cố định

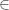
Xác định một vectơ chỉ phương
của
.
Phương trình tham số và phương trình chính tắc của
lần lượt có dạng
:
:
nếu
đều
Ví dụ : Viết phương trình tham số và phương trình chính tắc của đường thẳng đi qua hai điêm
và
Lời giải:
đi qua hai điểm
và
nên có vectơ chỉ phương
Vậy phương trình tham số của là:
Vậy phương trình chính tắc của là:
Dạng 2: Vị trí tương đối giữa hai đường thẳng  và
và  trong không gian
trong không gian
Phương pháp :
Xác định điểm cố định
và vectơ chỉ phương
của
.Xác định điểm cố định
và vectơ chỉ phương
của
.
Tính
.
Dùng các dấu hiệu sau để xét vị trí tương đối giữa
và
.
//

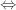



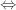
cắt

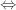
và
chéo nhau
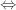
Ví dụ: Xét vị trí tương đối của đường thẳng là:
với đường thẳng
:
Lời giải:
Ta có đường thẳng đi qua điểm
và có vectơ chỉ phương
đi qua
và có vectơ chỉ phương
Ta có : .
Vậy và
chéo nhau.
Các em có thể lấy ví dụ về các trường hợp còn lại
Dạng 3: Vị trí tương đối giữa đường thẳng và mặt phẳng
Phương pháp :
Cho đường thẳng đi qua điểm
và vectơ chỉ phương
, cho mặt phẳng
có phương trình tổng quát
.
Gọi là VTPT của
.
Để xét vị trí tương đối giữa đường thẳng và mặt phẳng
ta có các cách sau:
Cách 1: Xét tích vô hướng
và thay tọa độ của điểm
vào phương trình của
để kiểm tra , ta có các trường hợp sau:

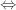
song song với
.

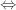
nằm trong
.

cắt
.

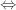
vuông góc với
.
Cách 2: Viết phương trình tham số của đường thẳng
:
Sau đó thay
ở phương trình tham số trên vào phương trình tổng quát của mặt phẳng
:
ta được:
hay
(1)
Xét số nghiệm
của phương trình (1) ta có các trường hợp sau.
vô nghiệm
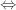
song song với
.
có mộy nghiệm
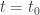
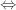
cắt
tại điểm
có vô số nghiệm
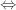
nằm trong
.
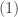

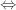
vuông góc với
.
Ví dụ: Xét vị trí tương đối của đường thẳng là:
với mặt phẳng
:
Lời giải:
Chuyển phương trình chính tắc của về phương trình tham số
:
Sau đó thay ở phương trình tham số trên vào phương trình tổng quát của mặt phẳng
:
Phương trình có một nghiệm
, vậy
cắt
tại điểm
Dạng 4: Tìm hình chiếu
Bài toán 1: Tìm hình chiếu vuông góc của điểm
trên đường thẳng
.
Phương pháp:
Cách 1: cho bởi phương trình tham số
suy ra dạng tọa độ của điểm
phụ thuộcvào tham số
- Tìm tham số
nhờ điều kiện
Cách 2: cho bởi phương trình chính tắc , gọi
(*)
: Biến đổi tỉ lệ thức này để dùng điều kiện (*), từ đó tìm được
Bài toán 2: Tìm hình chiếu vuông góc của điểm
trênặmt phẳng
.
Cách 1: Gọi
(*)
cùng phương với
: Biến đổi tỉ lệ thức này để dùng điều kiện (*) ,từ đó tìm được
.
Cách 2:
- Tìm phương trình đường thẳng
đi qua
và vuông góc với mặt phẳng
.
- Giao điểm của
và
chính là hình chiếu
của
trên mặt phẳng
.
Bài toán 3: Tìm hình chiếu vuông góc của đường thẳng
xuống mặt phẳng
.
- Tìm phương trình mặt phẳng
chứa đường thẳng
và vuông óc với mặt phẳng
.
- Hình chiếu
của
xuống mặt phẳng
chính là giao tuyến của
và
.
