Các bất đẳng thức quan trọng, thường dùng trong Toán cấp 3

Trong chương trình Toán cấp 3 có một số bất đẳng thức quan trọng và thường được dùng đó là: bất đẳng thức Cosi, bất đẳng thức Bunhiacopxki và bất đẳng thức Bernoulli…

Ngoài ra còn có bất đẳng thức Cauchy – Schward, bất đẳng thức Chebyshev, bất đẳng thức Jensen, bất đẳng thức Holder. Và một số bất đẳng thức mở rộng khác. Tuy nhiên trong bài này Toán cấp 3 chỉ tập trung vào các bất đẳng thức hay được sử dụng để giải toán nhất.

1. Bất đẳng thức Cosi

Trong toán học, bất đẳng thức Cosi là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Bất đẳng thức Cosi được phát biểu như sau:

Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
– Bất đẳng thức Cosi với 2 số a, b không âm: \[\frac{{a + b}}{2} \ge \sqrt {ab} \]

Dấu “=” xảy ra khi và chỉ khi \[a = b\]

– Bất đẳng thức Cosi với 2 số n không âm: \[\frac{{{x_1} + {x_2} + … + {x_n}}}{n} \ge \sqrt[n]{{{x_1}.{x_2}….{x_n}}}\]

Dấu “=” xảy ra khi và chỉ khi \[{x_1} = {x_2} = … = {x_n}\]

– Áp dụng bất đẳng thức Cosi chứng minh bất đẳng thức:

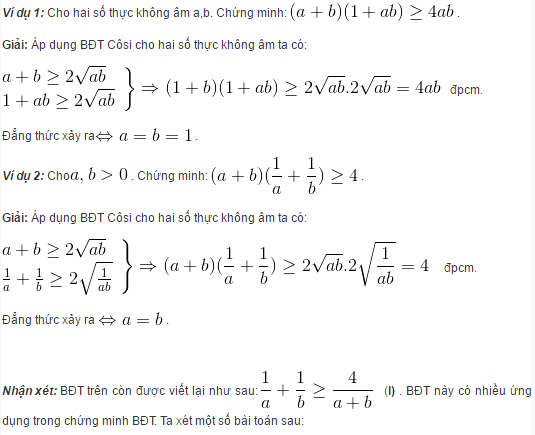
2. Bất đẳng thức Bunhiacopxki

– Bất đẳng thức Bunhiacopxky dạng đơn giản thường dùng:

\[(a_{}^2 + b_{}^2)(c_{}^2 + d_{}^2) \ge (ac + bd)_{}^2\]

Dấu “=” xảy ra khi và chỉ khi \[\frac{a}{c} = \frac{b}{d}\]

– Bất đẳng thức Bunhiacopxky cho 2 bộ số:

Với hai bộ số \[({a_1};{a_2};…{a_n}),({b_1};{b_2};…{b_n})\] ta có :

\[(a_1^2 + a_2^2 + … + a_n^2)(b_1^2 + b_2^2 + … + b_n^2) \ge ({a_1}{b_1} + {a_2}{b_2} + … + {a_n}{b_n})\]

Dấu “=” xảy ra khi và chỉ khi \[\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} – … = \frac{{{a_n}}}{{{b_n}}}\]

– Áp dụng bất đẳng thức Bunhiacopxky vào giải bất đẳng thức:

3.  Bất đẳng thức Bernoulli

Trong toán học, bất đẳng thức Bernoulli là một bất đẳng thức cho phép tính gần đúng các lũy thừa của 1 + x.

Bất đẳng thức này được phát biểu như sau: \[(1 + x)_{}^r \ge 1 + rx\]

với mọi số nguyên r ≥ 0 và với mọi số thực x > −1. Nếu số mũ r là chẵn, thì bất đẳng thức này đúng với mọi số thực x. Bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt như sau:

\[(1 + x)_{}^r > 1 + rx\]

với mọi số nguyên r ≥ 2 và với mọi số thực x ≥ −1 với x ≠ 0.

– Áp dụng bất đẳng thức Bernoulli vào giải bất đẳng thức: