Cách tìm giao điểm của đường thẳng và mặt phẳng

Để tìm giao điểm của đường thẳng và mặt phẳng thì các em cần phải có những kiến thức về lý thuyết thật vững.

Các kiến thức cần ghi nhớ là:

1. Đường thẳng thuộc mặt phẳng

Khi mặt phẳng có chứa ít nhất 2 điểm thuộc đường thẳng, tức là đường thẳng đi qua 2 điểm phân biệt của một mặt phẳng thì đường thẳng nằm trên mặt phẳng đó.

2. Cách xác định giao tuyến của hai mặt phẳng

Ta sẽ sử dụng phương pháp cách tìm giao tuyến của hai mặt phẳng ở bài trước.

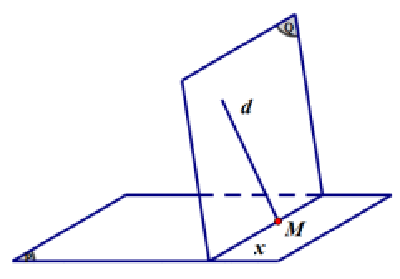
Phương pháp. Giả sử M là giao điểm của đường thẳng d và mặt phẳng (P), tức là M = d ∩ (P). Khi đó,

– M ∈ d (1)

– M ∈ (P) (2)

Gọi (Q) là mặt phẳng chứa đường thẳng d, d ⊂ (Q). Do đó, từ (1), M ∈ (Q) (3)

Từ (2) và (3), suy ra: M ∈ (P) ∩ (Q) hay M là điểm chung của hai mặt phẳng (P) và (Q). Như vậy, M thuộc đường giao tuyến x của hai mặt phẳng (P) và (Q), M∈ x (4).

Từ (1) và (4), suy ra: M ∈ d ∩ x, hay M là giao điểm của d và x.

Vậy thực chất của việc tìm giao điểm của đường thẳng với mặt phẳng là tìm giao điểm của đường thẳng với giao tuyến của hai mặt phẳng.

Với kết luận như trên, ta có được phương pháp tìm giao điểm như sau:

Để tìm giao điểm giữa đường thẳng d với mặt phẳng (P), ta thực hiện các bước:

– Tìm mặt phẳng phụ (Q) chứa đường thẳng d.

– Xác định giao tuyến x của mp (Q) và mp (P)

– Giao điểm M cúa x và d chính là giao điểm cần tìm.

Chúng ta thực hành làm bài tập tìm giao điểm của đường thẳng và mặt phẳng với các ví dụ dưới đây

Ví dụ 1: Cho hình chóp S.ABCD. Trên cạnh SC lấy một điểm E không trùng với điểm S và C. Tìm giao điểm của đường thẳng SD với mp(ABE).

Ví dụ 2: Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD. Tìm giao điểm của đường thẳng CD với mp (MNP).

Ví dụ 3: Cho hình bình hành ABCD, điểm S không nằm trong mặt phẳng (ABCD). Trên cạnh SC lấy điểm M. Tìm giao điểm của đường thẳng AM với mặt phẳng (SBD).

Ví dụ 4: Cho hình chóp S. ABCD có đáy là một hình bình hành, O là tâm của đáy; M, N lần lượt là trung điểm của SA, SC. Gọi (P) là mặt phẳng qua M, N và B. Tìm giao điểm I của đường thẳng SO với mp(P) và giao điểm K của đường thẳng SD với mp(P).

Ví dụ 5: Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).