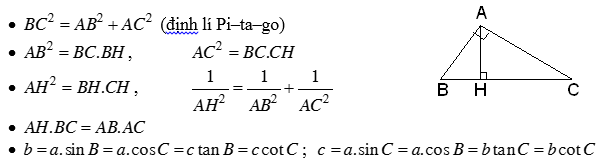Lý thuyết và bài tập hệ thức lượng trong tam giác

Lý thuyết về các hệ thức lượng trong tam giác

Ở bài viết này chúng ta nhắc lại các định lý và công thức cần ghi nhớ dưới đây:

Cho ΔABC có:

– Độ dài các cạnh: BC = a, CA = b, AB = c

– Độ dài các đường trung tuyến vẽ từ các đỉnh A, B, C: m_a, m_b, m_c

– Độ dài các đường cao vẽ từ các đỉnh A, B, C: h_a, h_b, h_c

– Bán kính đường tròn ngoại tiếp, nội tiếp tam giác: R, r

– Nửa chu vi tam giác: p

– Diện tích tam giác: S

Ta có các định lý và công thức về hệ thức lượng trong tam giác như sau:

1. Định lí côsin

$latex {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.\cos A$ ;

$latex {{b}^{2}}={{c}^{2}}+{{a}^{2}}-2ca.\cos B$ ;

$latex {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab.\cos C$

2. Định lí sin

$latex \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

3. Độ dài trung tuyến

$latex m_{a}^{2}=\frac{2({{b}^{2}}+{{c}^{2}})-{{a}^{2}}}{4}$ ;

$latex m_{b}^{2}=\frac{2({{a}^{2}}+{{c}^{2}})-{{b}^{2}}}{4}$ ;

$latex m_{c}^{2}=\frac{2({{a}^{2}}+{{b}^{2}})-{{c}^{2}}}{4}$

4. Diện tích tam giác

S = $latex \frac{1}{2}a{{h}_{a}}=\frac{1}{2}b{{h}_{b}}=\frac{1}{2}c{{h}_{c}}$

= $latex \frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C$

= $latex \frac{abc}{4R}$

= $latex pr$

= $latex \sqrt{p(p-a)(p-b)(p-c)}$ (công thức Hê–rông)

Giải tam giác là tính các cạnh và các góc của tam giác khi biết một số yếu tố cho trước.

5. Hệ thức lượng trong tam giác vuông (nhắc lại)

Cho ΔABC vuông tại A, AH là đường cao.

* Chú ý: Ghi nhớ định lý Pitago để chứng minh một tam giác là vuông.

6. Hệ thức lượng trong đường tròn (bổ sung)

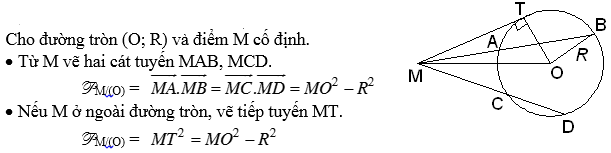
Bài tập hệ thức lượng trong tam giác

Bài 1: Chứng minh rằng trong mọi tam giác ABC ta có;

a) $latex a=b.\cos C+c.\cos B$

b) $latex \sin A=\sin B\cos C+\sin C\cos B$

c) $latex {{h}_{a}}=2R\sin B\sin C$

d) $latex m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=\frac{3}{4}({{a}^{2}}+{{b}^{2}}+{{c}^{2}})$

e) $latex {{S}_{\Delta ABC}}=\frac{1}{2}\sqrt{A{{B}^{2}}.A{{C}^{2}}-{{\left( \overrightarrow{AB}.\overrightarrow{AC} \right)}^{2}}}$

Bài 2: Cho tam giác ABC. Chứng minh rằng:

a) Nếu b + c = 2a thì $latex \frac{2}{{{h}_{a}}}=\frac{1}{{{h}_{b}}}+\frac{1}{{{h}_{c}}}$

b) Nếu bc = a² thì $latex \sin B\sin C={{\sin }^{2}}A,\,\,{{h}_{b}}{{h}_{c}}=h_{a}^{2}$

c) A vuông ⇔ $latex m_{b}^{2}+m_{c}^{2}=5m_{a}^{2}$

Bài 3: Cho tứ giác lồi ABCD, gọi a là góc hợp bởi hai đường chép AC và BD.

a) Chứng minh diện tích S của tứ giác cho bởi công thức: $latex S=\frac{1}{2}AC.BD.\sin \alpha $ .

b) Nêu kết quả trong trường hợp tứ giác có hai đường chéo vuông góc.

Bài 4: Cho DABC vuông ở A, BC = a, đường cao AH.

a) Chứng minh $latex AH=a.\sin B.\cos B,\,\,BH=a.{{\cos }^{2}}B,\,\,CH=a.{{\sin }^{2}}B$

b) Từ đó suy ra $latex A{{B}^{2}}=BC.BH,\,\,A{{H}^{2}}=BH.HC$

Bài 5: Cho DAOB cân đỉnh O, OH và OK là các đường cao. Đặt OA = a, $latex \widehat{AOH}=\alpha $ .

1. a) Tính các cạnh của ΔOAK theo a và α.
2. b) Tính các cạnh của các tam giác OHA và AKB theo a và a.
3. c) Từ đó tính $latex \sin 2\alpha ,\,\,\cos 2\alpha ,\,\,\tan 2\alpha $ theo $latex \sin \alpha ,\,\,\cos \alpha ,\,\,\tan \alpha $ .

Bài 6: Giải tam giác ABC, biết:

a) $latex c=14;\,\,\widehat{A}={{60}^{0}};\,\,\widehat{B}={{40}^{0}}$

b) $latex b=4,5;\,\,\widehat{A}={{30}^{0}};\,\,\widehat{C}={{75}^{0}}$

c) $latex c=35;\,\,\widehat{A}={{40}^{0}};\,\,\widehat{C}={{120}^{0}}$

d) $latex a=137,5;\,\,\widehat{B}={{83}^{0}};\,\,\widehat{C}={{57}^{0}}$

Bài 7: Giải tam giác ABC, biết:

a) $latex a=6,3;\,\,b=6,3;\,\,\widehat{C}={{54}^{0}}$

b) $latex b=32;\,\,c=45;\,\,\widehat{A}={{87}^{0}}$

c) $latex a=7;\,\,b=23;\,\,\widehat{C}={{130}^{0}}$

d) $latex b=14;\,\,c=10;\,\,\widehat{A}={{145}^{0}}$

Bài 8: Giải tam giác ABC, biết:

a) $latex a=14;\,\,b=18;\,\,c=20$

b) $latex a=6;\,\,b=7,3;\,\,c=4,8$

c) $latex a=4;\,\,b=5;\,\,c=7$

d) $latex a=2\sqrt{3};\,\,b=2\sqrt{2};\,\,c=\sqrt{6}-\sqrt{2}$