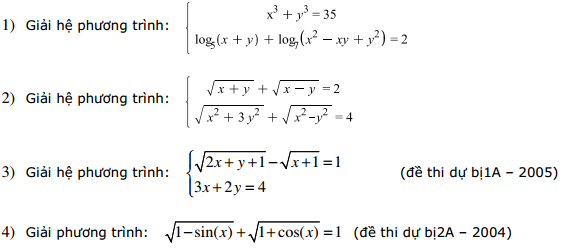Ứng dụng phương trình đường thẳng để giải phương trình căn thức
Toán cấp 3 giới thiệu với em cách ứng dụng phương trình đường thẳng để giải phương trình căn thức qua các ví dụ. Có nếu ra phương pháp giải dễ hiểu.
Trước tiên chúng ta cần nhắc lại kiến thức về đường thẳng.
Tóm tắt
1. Hai dạng phương trình đường thẳng
a) Phương trình tổng quát
Đường thẳng đi qua M(x0;y0) và có vectơ pháp tuyến $latex \displaystyle \overrightarrow{n}$(A;B) thì đường thẳng đó có phương trình:
(d): A(x-x0)+B(y-y0)=0
⇔ (d): Ax+By+C=0
VD1: Đường thẳng qua M(1;2) nhận $latex \displaystyle \overrightarrow{n} (2;1) làm vectơ pháp tuyến.
(d): 2(x-1)+1(y-2)=0
⇔ (d): 2x+y-4=0
b) Phương trình tham số
Đường thẳng đi qua M(x0;y0) và có vectơ chỉ phương $latex \displaystyle \overrightarrow{a}$(a1;a2)
(d): $latex \displaystyle \left\{ \begin{array}{l}x={{x}_{0}}+{{a}_{1}}t\\y={{y}_{0}}+{{a}_{2}}t\end{array} \right.$
VD2: Đường thẳng qua M(3;4) nhận $latex \displaystyle \overrightarrow{a}$(2;3) làm vectơ pháp tuyến có phương trình:
(d): $latex \displaystyle \left\{ \begin{array}{l}x=3+2t\\y=4+3t\end{array} \right.$
VD3: Cho (d): x+y=4. Viết phương trình tham số của (d).
Giải:
Vectơ pháp tuyến : $latex \displaystyle \overrightarrow{n}$(1,1)
Vectơ chỉ phương : $latex \displaystyle \overrightarrow{a}$(1,-1)
Điểm đi qua M(2;2)
⇒ (d): $latex \displaystyle \left\{ \begin{array}{l}x=2+t\\y=2-t\end{array} \right.$
2. Ví dụ ứng dụng
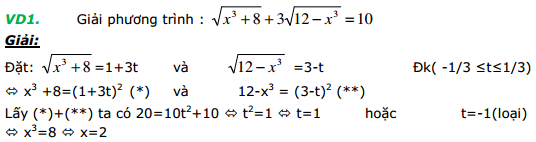
Có phải bạn đang tự hỏi: thuật toán nào đã giúp ta nhìn thấy được cách đặt ẩn t ???
Không phải ngẫu nhiên mà tôi lại trình bày lại vấn đề đường thẳng, một vấn đề tưởng chừng như chẳng liên quan gì đến đại số. Nhưng giờ đây ta mới nhận ra được “đường thẳng” chính là “tuyệt chiêu” để giải phương trình dạng căn thức. Mấu chốt đó là:
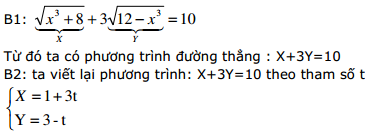
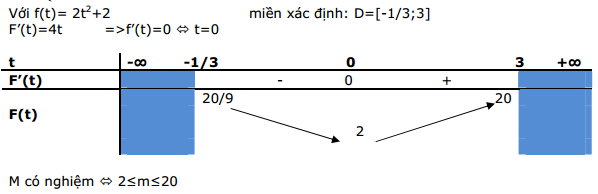
Lúc này phương trình đã quy về 1 ẩn t và việc giải phương trình trên là không khó. (Vì đây là kiến thức “lớp nhí”)
Để hiểu rõ hơn về phương pháp này các bạn hãy cùng tôi đến với VD2.



3. Bài tập tự luyện