Lý thuyết hàm số bậc 2
Lý thuyết hàm số bậc 2
1. Định nghĩa hàm số bậc 2
Hàm số bậc hai là hàm số có công thức: [latex]\displaystyle y=ax_{{}}^{2}+bx+c[/latex] ( với a ≠ 0)
Tập xác định (TXĐ): D = R.
2. Tính biến thiên của hàm số bậc 2
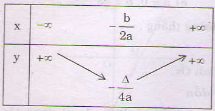
Bảng biến thiên của hàm số:
a > 0 hàm số nghịch biến trên [latex]\displaystyle \left( {-\infty ;-\frac{b}{{2a}}} \right)[/latex] và đồng biến trên khoảng [latex]\displaystyle \left( {-\frac{b}{{2a}};+\infty } \right)[/latex]
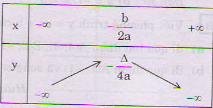
a < 0 hàm số đồng biến trên [latex]\displaystyle \left( {-\infty ;-\frac{b}{{2a}}} \right)[/latex] và nghịch biến trên khoảng [latex]\displaystyle \left( {-\frac{b}{{2a}};+\infty } \right)[/latex]
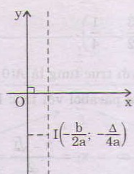
Đồ thị hàm số [latex]\displaystyle y=ax_{{}}^{2}+bx+c[/latex] là một đường parabol (P) có:
Tọa độ đỉnh I [latex]\displaystyle \left( {\frac{{-b}}{{2a}};f\left( {\frac{{-b}}{{2a}}} \right)} \right)[/latex]
với [latex]\displaystyle {f\left( {\frac{{-b}}{{2a}}} \right)}[/latex] = [latex]\displaystyle \frac{{-\Delta }}{{4a}}[/latex]
Trục đối xứng : x = [latex]\displaystyle \frac{{-b}}{{2a}}[/latex]
Parabol (P) quay bề lõm lên trên nếu a > 0, parabol (P) quay bề lõm xuống dưới nếu a < 0 . Dựa vào bảng biến thiên ta có thể hình dung được hình dáng của đồ thị.
Nguồn: Trường cao đẳng y Dược Pasteur