Bài giảng khảo sát và vẽ đồ thị hàm số hay, chi tiết

Bài giảng khảo sát đồ thị hàm số hay và chi tiết bao gồm dạng  khảo sát đồ thị hàm số bậc 3 và bậc 4 (trùng phương), bậc nhất trên bậc nhất.

Bài giảng được liệt kê chi tiết từng bước làm cụ thể và hướng dẫn cách trình bày một cách cẩn thận giúp các em học sinh nắm vững được phương pháp làm bài và vững cả cách trình bày, để không mất điểm ở môn Toán trong kỳ thi THPT quốc gia, tuyển sinh đại học. Ngoài ra còn có các dạng bài thường gặp trong kỳ thi.

1. Khảo sát và vẽ đồ thị hàm số bậc 3

[latex]\displaystyle y=ax_{{}}^{3}+bx_{{}}^{2}+cx+d[/latex]

– Ví dụ 1: Khảo sát và vẽ đồ thị hàm số: [latex]\displaystyle y=x_{{}}^{3}+3x_{{}}^{2}-4[/latex]
– Ví dụ 2: Khảo sát và vẽ đồ thị hàm số: [latex]\displaystyle y=\frac{{x_{{}}^{3}}}{3}-x_{{}}^{2}+x+1[/latex]
– Ví dụ 3: Khảo sát và vẽ đồ thị hàm số: [latex]\displaystyle y=-x_{{}}^{3}+3x_{{}}^{2}-4x+2[/latex]

Giải ví dụ 1:

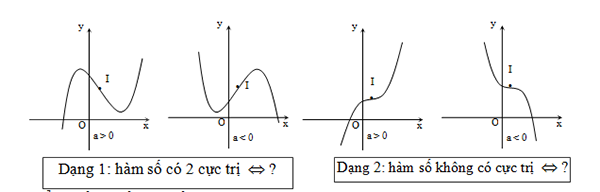
Bốn dạng đồ thị của hàm số bậc 3:

2. Khảo sát và vẽ đồ thị hàm số trùng phương

[latex]\displaystyle y=ax_{{}}^{4}+bx_{{}}^{2}+c[/latex]

– Ví dụ 1: Khảo sát và vẽ đồ thị của hàm số: [latex]\displaystyle y=x_{{}}^{4}-2x_{{}}^{2}-3[/latex]

– Ví dụ 2: Khảo sát và vẽ đồ thị của hàm số: [latex]\displaystyle y=-\frac{{x_{{}}^{4}}}{2}-x_{{}}^{2}+\frac{3}{2}[/latex]

– Ví dụ 3: Khảo sát và vẽ đồ thị của hàm số: [latex]\displaystyle y=-x_{{}}^{4}+2x_{{}}^{2}-2[/latex]

Giải ví dụ 1:

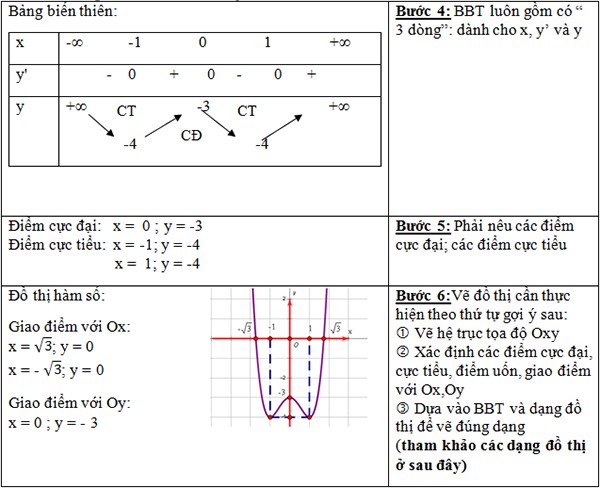
Tương tự các em học sinh giải những ví dụ 2, 3 còn lại.

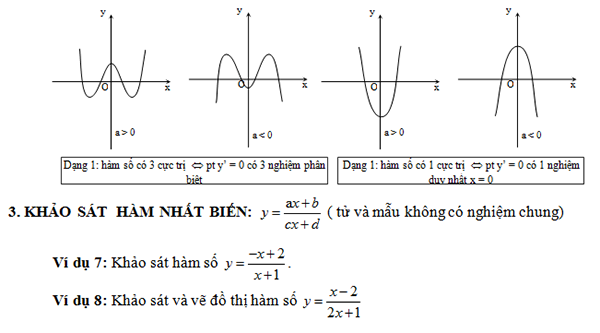
Bốn dạng đồ thị của hàm số trùng phương

Giải ví dụ 7:

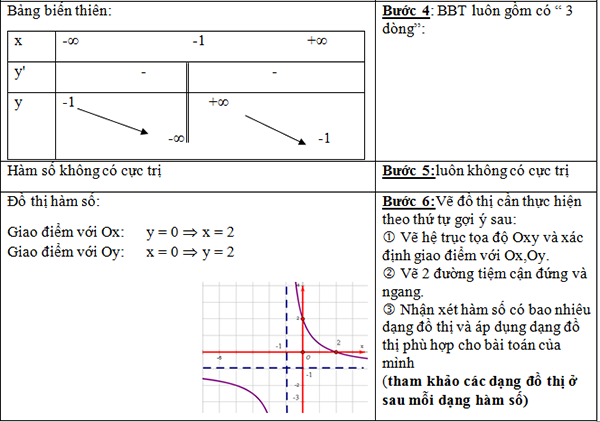
Các em giải ví dụ 8 và 9

Hai dạng đồ thị của hàm số nhất biến:

* Bài tập thực hành khảo sát và vẽ đồ thị hàm số

Bài 1. Cho hàm số [latex]\displaystyle y=x_{{}}^{3}-4x+2[/latex] (C)

a) Khảo sát và vẽ đồ thị (C) của hàm số trên

b) Dựa vào đồ thị (C) , biện luận theo m số nghiệm thực của phương trình: [latex]\displaystyle x_{{}}^{3}-4x+2-m=0[/latex]

c) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm H(1;2)

d) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x =3/2

e) Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ y = 0

Bài 2. Cho hàm số [latex]\displaystyle y=-x_{{}}^{3}+3x_{{}}^{2}-4[/latex] (C)

a) Khảo sát và vẽ đồ thị (C) của hàm số .

b) Dựa vào đồ thị (C) , biện luận theo m số nghiệm thực của phương trình:

[latex]\displaystyle x_{{}}^{3}-3x_{{}}^{2}+m=0[/latex]

c) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ là x = 3/2